SOLIDWORKS Simulation VS Hand Calculations
SOLIDWORKS Simulation is a very powerful tool capable of a range of broad studies. When discussing simulation, we are often asked about the accuracy of the results. SOLIDWORKS works with NAFEMS (National Agency for Finite Element Methods and Standard) to validate the code against industry problems. These can be reviewed by going to Help>SOLIDWORKS Simulation>Validation>NAFEMS Benchmark
The blog below goes through one of these examples, a Cantilever beam problem. Below I will show a comparison against the hand calculations and SOLIDWORKS
The Problem
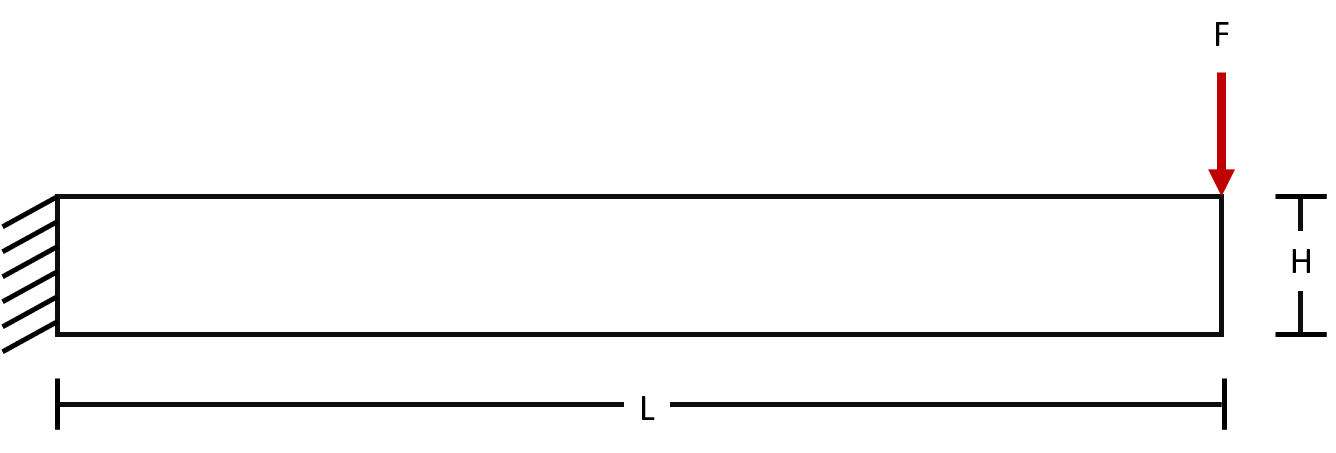
The beam is to be supported at one end and free at the other, there is a load applied downwards at the free end of the beam. We want to find out what the deflection at the end of the beam will be and the Stress at the supported end.
The given values-
Force (F): 4500N
Length (L): 1m
Elastic Modulus (E): 2.1×1011 N/m2
Thickness (T): 10mm
Height (H): 80mm
Poisson ratio :0
Hand Calculations
To work out the displacement and stress, 4 equations will be needed.
Deflection- Δ=FL/3EI
Where the equation for Second moment of inertia- I=(TH3)/12
Stress at support- Stress=FL/Z
Where:-
Z=I/(Distance from neutral axis to edge)
Calculations for I-
I=(0.01*〖0.08〗3)/12
I=4.2667×107 m4
Deflection-
Δ=(4500*1)/(3*(2.1×1011 )*(4.2667×107))
Δ=4500/268800 Δ=0.016741m
Solving for Z-
Z=(4.2667×107)/0.04
Z=1.06 ̇×10-5m3
Solving for Stress at support-
Stress=4500/(1.06 ̇×10-5 )
Stress= 4.218×108N/m2
SOLIDWORKS
The beam can be modelled as a 3D shape or represented as a surface, making use of SOLIDWORKS Shell meshing. Shell meshing can greatly reduce the calculation time for suitable studies, the beam is modelled below with the following dimensions (mm).

Next a Static study was created in the Simulation module.
The material properties given in the problem are the elastic modulus and Piossons ratio. I have created a custom material with these qualities and applied it to the surface.
Unlike with 3D meshes the thickness of the model has to be defined in the definition of the shell. For this example, the Cantilever beam is 10mm thick. Right click the part in the simulation window and add this to the definition.
Our model now represents the beam in the problem, now the fixture and load can be applied. The left most edge is where the beam connects to the wall. This will have no translation or rotation so a standard fixed geometry can be used here.
The force is being applied to the right edge of the beam to add the correct for a direction needs to be added using a reference plane. The front plane and along the plane were used.

Run the study
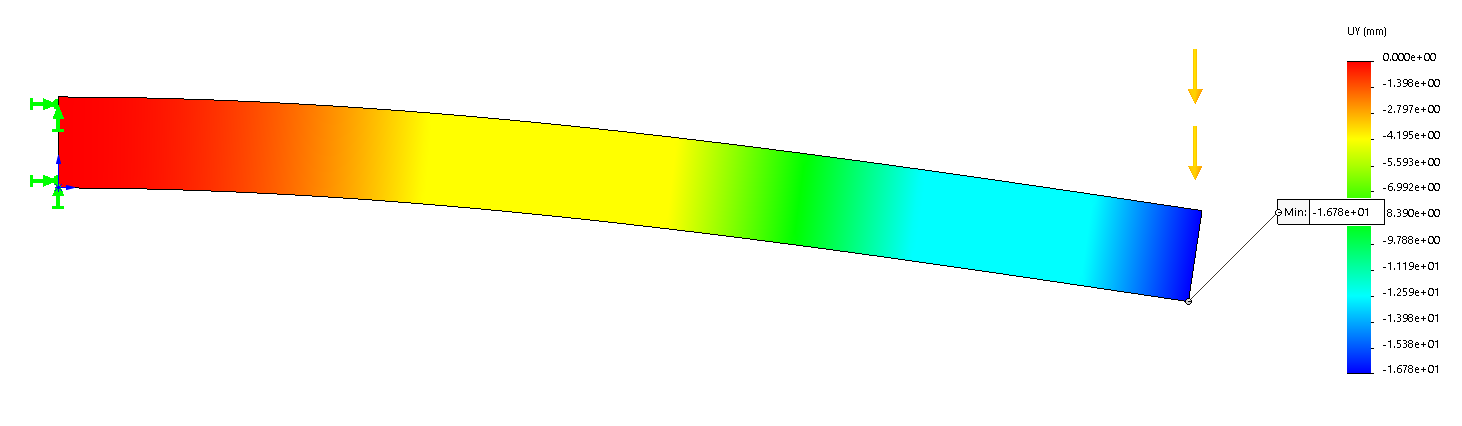
Below is the Normal stress plot for X axis with a max stress of 4.22×108 N/m2. Showing the max stress located at the supported end of the beam.
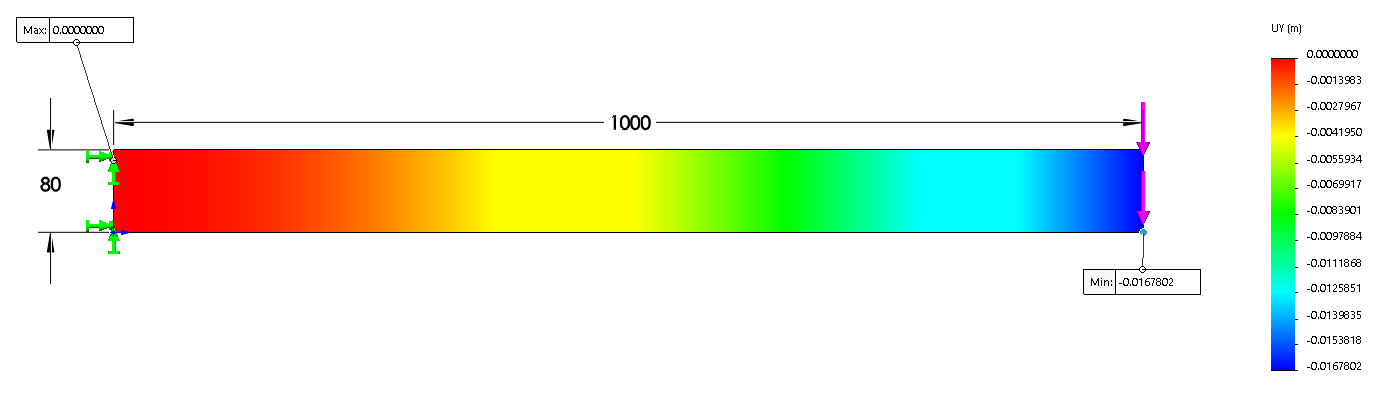
Plot showing the displacement in the Y direction, with a max displacement of 0.0167m at the unsupported end of the beam.
Evaluation
|
|
Hand Calcs |
Simulation |
Percentage difference |
|
Stress |
4.218×108( N/m2) |
4.224×108 (N/m2) |
0.14 |
|
Displacement |
0.016741(m) |
0.0167802(m) |
0.24 |
This simple exercise validates the SOLIDWORKS simulation software against theoretical hand calculations. These exercises are useful in understanding the software and understanding how it can assist in the design process by making virtual testing easy.
To find out more on SOLIDWORKS Simulation, please Click Here

